Summer School
Information about the second part of the BIP
22 - 26 May 2023
Summer School with mini-courses and talks given by experts, to be held during the week 22-26 May 2023 in presence at the Math Department of Bologna University, located in Piazza di Porta San Donato 5.
The lectures will take place in the room named Aula Vitali, at the ground floor of the building.
Schedule:
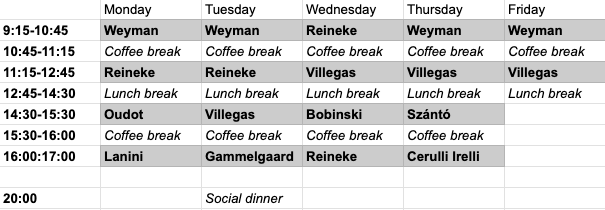
Mini-courses:
Ruhr-Universität Bochum
Moduli spaces of quiver representations
We will first work through the construction of moduli spaces of quiver representations as GIT quotients, and collect basic geometric properties. We will then work out classes of examples where these spaces can be described explicitly. We will describe geometric techniques for studying moduli spaces, for example coordinates, vector bundles, torus localization, Hilbert scheme.
Jagiellonian University
Semi-invariants of quivers and their applications
I will discuss the semi-invariants of quiver representations and their applications. After providing some background on invariant theory and representations of general linear groups I will discuss the Schofield determinantal semi-invariants and the theorem stating that they span all semi-invariants. The next topic will be the structure of rings of semi-invariants depending on representation type of the quiver. The applications will include the saturation theorem for semi-invariants, its consequences for Littlewood-Richardson coefficients. If time permits I will discuss the bounds for degrees of generating semi-invariants and connection to complexity theory.
International Centre for Theoretical Physics (ICTP)
Counting representations of quivers over finite fields
In these lectures I will present the calculation of the title in the case of the star-shaped quivers related to character varieties based on my joint work with E. Letellier and T. Hausel. The starting point will be a formula of Hua for a general quiver. The basic tool used is the combinatorics of symmetric functions and generating functions, which I will discuss from scratch.
Speakers:
Grzegorz Bobinski
Nicolaus Copernicus University Toruń
On studying normality problems for varieties of quiver representations
There are natural subsets of varieties of quiver representations, whose normality is an object of study. Examples are the orbit (= isomorphism classes) closures and (irreducible components of) varieties of representations of bound quivers. A general strategy to prove normality is to use Serre's criterion, which implies that a Cohen-Macaulay variety is normal if and only if it is nonsingular in codimension one. While a reformulation in terms of representation theory of the fact that a subset of a variety of quiver representations is Cohen-Macaulay seems to be unknown, there is an interpretation of tangent spaces in terms of extensions due to Voigt. Using this interpretation one obtains representation-theoretic tools which can be used in order to study nonsingularity (in codimension one). The aim of the talk is to present and illustrate by examples two such tools, i.e. hom-schemes (due to Riedtmann and Zwara) and ext-schemes (due to the speaker).
Giovanni Cerulli Irelli
Sapienza - Università di Roma
Motzkin combinatorics in linear degenerations of the flag variety
In 2021 Fang and Reineke described the support of linear degenerations of flag varieties in terms of Motzkin paths, by using Knight-Zelevinsky multi-segment duality. In a joint project with Esposito and Marietti (IMRN 2023, arXiv 2206.10281) we give a new characterization of supports in representation-theoretic terms by what we call excessive multi-segments. To do so we consider an algebraic structure on the set of Motzkin paths that we call Motzkin monoid. By using a universal property of the Motzkin monoid, we show that excessive multi segments are parametrized in a natural way by Motzkin paths. Moreover, we show that this parametrization coincides exactly with the Fang-Reineke parametrization. As a byproduct we have an elementary combinatorial criterion to decide if a multisegment is a support. We have an inductive procedure to describe the inverse of the Fang-Reineke map. In this term there is a very beautiful (as yet conjectural) formula for the coefficients.
Søren Gammelgaard
SISSA Trieste
Quiver representations and surface singularities
Let G be a finite subgroup of SL_2 (C). With the tautological action of G on A^2, we can construct the singularity A^2/G and its minimal resolution. To these surfaces, we can associate several different interesting schemes, such as their symmetric powers, their punctual Hilbert schemes, and moduli spaces of framed torsion-free sheaves. We will talk about how these can be understood as quiver varieties constructed from a simple quiver associated to G by the McKay correspondence. Some of this is joint work with A. Craw, B. Szendrői, and A. Gyenge.
Martina Lanini
Università degli Studi di Roma Tor Vergata
Symmetric quivers and symmetric varieties
In this talk I will report on ongoing joint work with Ryan Kinser and Jenna Rajchgot on varieties of symmetric quiver representations. These varieties are acted upon by a reductive group via change of basis, and it is natural to ask for a parametrisation of the orbits, for the closure inclusion relation among them, for information about the singularities arising in orbit closures. Since the Eigthies, same (and further) questions about representation varieties for type A quivers have been attached by relating such varieties to Schubert varieties in type A flag varieties (Zelevinsky, Bobinski-Zwara, ...). I will explain that in the symmetric setting it is possible to interpret the above questions in terms of certain symmetric varieties. More precisely, we show that singularities of an orbit closure of a symmetric quiver representation variety are smoothly equivalent to singularities of an appropriate Borel orbit closure in a symmetric variety.
Steve Oudot
INRIA Paris, École Polytechnique
Quiver Representations in Topological Data Analysis
This talk will be an introduction to the field of topological data analysis, emphasizing the role played in it by quiver representation theory. Specifically, I will describe how the supports of the indecomposables can be used as descriptors for data, with stability guarantees under suitable choices of metrics on the representation categories of the quivers under consideration. I will also explain how one proceeds when those quivers are of wild representation type.
Csaba Szántó
Babes-Bolyai University Cluj-Napoca
Ringel-Hall polynomials associated to tame quivers
Classical Hall algebras associated with discrete valuation rings were introduced by Steinitz and Hall to provide an algebraic approach to the classical combinatorics of partitions. The multiplication is given by Hall polynomials which play an important role in the representation theory of the symmetric groups and the general linear groups. In 1990 Ringel defined Hall algebras for a large class of rings, namely finitary rings, including in particular path algebras of quivers over finite fields. Far reaching analogues of the classical ones, these Ringel-Hall algebras provided a new approach to the study of quantum groups using the representation theory of finite dimensional algebras. They can also be used successfully in the theory of cluster algebras or to investigate the structure of the module category.
In case of Ringel-Hall algebras corresponding to Dynkin quivers and tame quivers we know due to Ringel and Hubery, that the structure constants of the multiplication are again polynomials in the number of elements of the base field. These are the Ringel-Hall polynomials. If we are looking at Hall polynomials associated to indecomposable modules, the classical ones are just 0 or 1, the Ringel-Hall ones in the Dynkin case are also known and have degree up to 5. However we do not have too much information about the Ringel-Hall polynomials in the tame cases.
In the first part of the talk we survey the indecomposable representations of tame quivers over finite fields. The second part is dedicated to the presentation of our tools and results related to the determination of tame Ringel-Hall polynomials associated to indecomposables.

